Jump back to one of the following links:    Home     Courses   Tutorials      Misc

Jump to one of the following dimensional analysis parts:   Choose One Introduction to Dimensional Analysis Part 1- The Need for Units Part 2- Setting up Conversions Part 3- Basic Conversion Problems Part 4- Complex Conversion Problems Part 5- Problem Dissection I Part 6- Problem Dissection II Part 7- Density Problems Part 8- Quizzes

Before you can calculate just how many inches there are in a kilometer or how many milliliters there are in a quart, you need to be able to write basic conversions. In my class, I don't require too much memorization in this area. I do require that six basic metric prefixes be memorized (mega, kilo, deci, centi, milli, and micro) since prefixes are useful across the entire metric system and not just for length measurements, for example.

Here's a basic list of unit conversions.

Conversions within a unit system are exact. There are exactly 12 inches in one foot, 4 quarts in one gallon, 1000 milliliters in 1 liter (or 0.001 L in 1 mL), 1000 grams in 1 kilogram, etc. When evaluating your answer for the proper number of significant figures, you essentially ignore the exact unit conversions. Unit conversions across unit systems, as in metric to standard, aren't necessarily exact. There are exactly 2.54 centimeters in 1 inch. But, there are 453.59 grams in one pound and since this is rounded to 2 decimal places, there are 5 significant figures (you think of it as being approximately 453.59 grams in exactly 1 pound).

Once you've picked any conversions you need for a problem, how do you set it up? You go from equivalencies, the way they are displayed in the unit conversion list, to fractions. For example, here's the conversion between meters and millimeters shown as fractions-

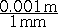
  or  

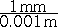
All conversions work this way. The next section will help you learn how to choose the proper conversion set up based on what's given and what's desired.